Hallo zur Webseite von
DL1DMW
DL1DMW

<- Bild 1: MicroCAP 12 zeigt links eine Filterkurve, rechts den Schaltplan des NF-Verstärkers.
Monte-Carlo-Analyse mit
MicroCAP12
MicroCAP ist das professionelle – und inzwischen für alle frei gegebene – Simulationsprogramm für analoge und digitale Schaltungen auf der Basis von SPICE. Neben einigen Basics, die bei der Nutzung des Programms zu beachten sind, soll gezeigt werden, wie sich Bauteiltoleranzen auf die Funktion einer Schaltung simulieren lässen.
MicroCAP-Basics – eine Einführung
Neueinsteiger sollten etwas Grundwissen mitbringen, damit es mit der Simulation – das Benutzerhandbuch spricht präziser von Analysen - klappt. Das über 200-seitige, englischsprachige Handbuch (User-Guide) ist als erste Lektüre sehr zu empfehlen.
Das detailliertere Reference-Manual zählt fast 1100 Seiten! Dennoch lohnt zum Einstieg eine kurze Einführung auf wenigen Seiten: Alles beginnt mit der Platzierung der Komponenten auf dem Schaltplan-Arbeitsblatt. Für Bauteile wie Widerstand, Kondensator, Spule, Diode etc. stehen in der Funktionsleiste entsprechende Symbole bereit. Ebenso findet man derlei Bauteile unter Analog Primitives links im MicroCAP-Fenster wie auch im Menü Component / Analog Primitives / Passiver Components. Legt man ein Bauelement mit der Maus auf der Arbeitsfläche ab, öffnet sich der Eigenschaften-Dialog und ein Cursor blinkt zur Eingabe des Wertes. Hierbei ist die Syntax strikt zu beachten
Eingabesyntax:
 Ein großes M bedeutet also Milli und nicht, wie man vermuten könnte Mega! Reelle Zahlen werden nicht mit dem Komma, sondern mit dem Punkt geschrieben (statt 4,7k also 4.7k), Sie können aber auch 4k7 schreiben.
Ein großes M bedeutet also Milli und nicht, wie man vermuten könnte Mega! Reelle Zahlen werden nicht mit dem Komma, sondern mit dem Punkt geschrieben (statt 4,7k also 4.7k), Sie können aber auch 4k7 schreiben. <- Bild 2: Wahl einer Spannungs- oder Stromquelle über das Menü Components / Analog Primitives.
Sie verlassen den Dialog mit der Taste <ENTER> oder über den Button OK. Fügen Sie über Components / Analog Primitives / Waveform Sources eine Spannungsquelle oder einen Sinusgenerator hinzu (Bild 2).
Wir bauen für eine erste Simulation einen einfachen Tiefpass aus Widerstand (4k7), Kondensator (1u) und einer Sinusquelle in Serie. Geben Sie bei letzterer unter Value einen Wert von 10 kHz an.
Jede Schaltung benötigt ein Massesymbol (Ground), ohne das eine korrekte Simulation nicht möglich ist. Nun verdrahten Sie die Bauelemente miteinander. Aktivieren Sie zuerst im Menü Options / View die Anzeige Pin Numbers und Knotennummern (Node Numbers). Damit erkennen Sie, ob Bauelemente korrekt mit dem „Draht“ verbunden sind. Knotennummern werden nach der Simulation bzw. Analyse bedeutsam. Schalten Sie nun mit STRG+W (oder über das Drahtsymbol in der Funktionsleiste) in den Drahtmodus (wire mode) und verbinden die Bauelemente untereinander. Das geschieht intuitiv. Unsere simple Schaltung könnte auf ihrem Monitor etwa so aussehen (Bild 3).
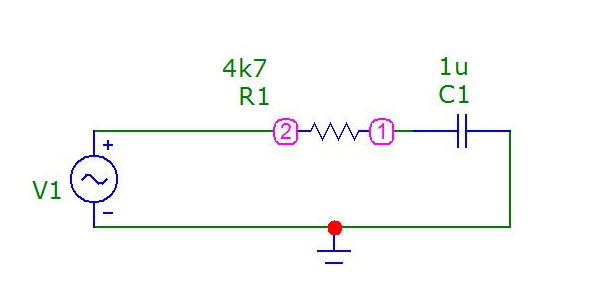
Bild 3: Das Schaltbild des einfachen RC-Gliedes als Tiefpass.
Möchten Sie den Wert bzw. die Eigenschaften eines Bauteils nachträglich ändern, gelangen Sie in das Eigenschaftenfenster mit einem Doppelklick auf das Bauelement.
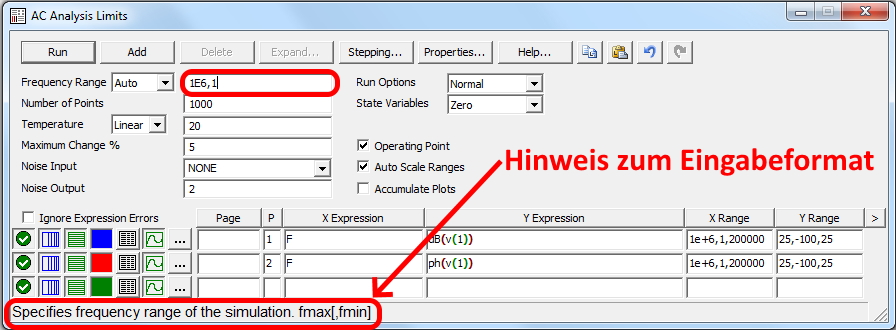
Bild 4: Dialog zur AC-Simulation. Die Zeile unten gibt wichtige Hinweise zur Eingabesyntax.
Starten Sie aus Interesse eine Transienten-Analyse (Menü Analysis / Transient). Das entspricht der Darstellung eines Oszilloskops. Belassen Sie alle Parameter, wie sie das Programm eingetragen hat und starten mit Run. Erwartungsgemäß zeigt die Analyse eine Sinusschwingung. Beachten Sie bitte: Die Menüleiste weist neue Menüs wie Transient, Scope und Monte Carlo auf, die weitere Funktionen bieten. Beenden Sie die Analyse durch Schließen des Fensters oder klicken im Menü Transient auf Exit Analysis oder betätigen die Funktionstaste F3.
Wir können nun, um den Effekt des Tiefpasses zu erkennen, eine erste AC-Analyse starten. Im Menü Analysis / AC oder mit ALT+2 öffnet sich der Dialog zur Eingabe der Simulationsparameter (Bild 4). Bei der Wechselstrom-Simulation des Tiefpasses ist die Vorgabe des Frequenzbereiches maßgeblich. Dabei muss im Feld Frequency Range die Syntax eingehalten werden: Zuerst wird die höhere Frequenz in Hz, gefolgt von einem Komma die niedrige Frequenz in Hz angegeben, wie Bild 4 verdeutlicht (1E6 Hz = 1000000 Hz = 1 MHz). Ein Klick bei Auto Scale Ranges bewirkt eine automatische Skalierung beider Achsen des Bode-Plots.
Gehen Sie mit der Maus auf Entdeckungskurs: Ändern Sie die X-Skalierung von logarithmisch zu linear, verändern Sie die Form der Ausgabe vom Bode-Plot zur Polardarstellung oder einem Smithdiagramm oder verändern die Zeichenfarbe des Graphen. Schauen Sie sich die Parameter der Spalten X- und Y-Expressions an, die erscheinen, sobald Sie in einem der Eingabefelder die rechte Maustaste betätigen. Erkunden Sie die Möglichkeiten des Kontextmenüs.
In den Spalten X- und Y-Expression trägt man die zu berechnenden Formeln ein. Hier hat es das Programm bereits erledigt. Die X-Achse enthält nur ein „F“ und damit wird auf der X-Achse die Frequenz aufgetragen. Die Y-Achse ist mit dB(v(1)) belegt. Die „1“ bezieht sich dabei auf die Knotennummer (node number), die Sie im Schaltplan sehen. Am Ende starten Sie die Analyse mit Run.

Bild 5: Frequenz und Phase des Tiefpassfilters in Bode-Darstellung.
Das Resultat der Analyse zeigt Bild 5. Oben sehen Sie den Frequenzgang, darunter den Phasengang. Möchten Sie Parameter der Analyse verändern? Mit F9 öffnet sich der Dialog erneut. Weitere Funktionen bietet das Menü AC.
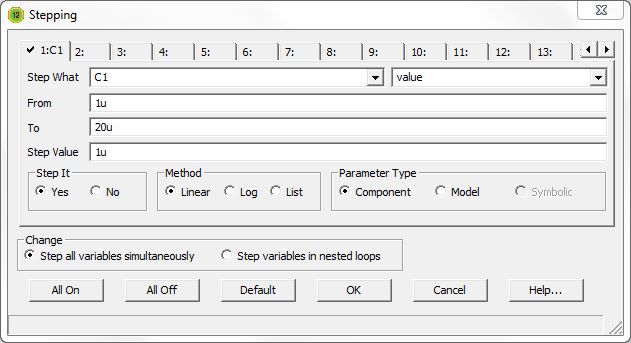
Bild 6: In dem Stepping-Dialog legt man eines oder mehrere Bauelemente fest, deren Wert bei der Analyse verändert werden.

Bild 7: Dia Analyse bei Variation von C1 zeigt die sich ergebende Kurvenschar für Werte zwischen 1µF und 20µF
Stepping
Im Parameter-Dialog zu den Analysen gibt es oben einen Button Stepping (Bild 4). Hier bietet sich die Möglichkeit, Bauteilewerte in der Simulation zu verändern. Wir wollen den Wert des Kondensators von 1µF zwischen 1µF und 20µF variieren und das Ergebnis grafisch ausgeben lassen. In dem Stepping-Dialog (Bild 6) wählen Sie unter Step What den Kondensator C1 aus und tragen die Werte From und To wie in Bild 6 ein. Nach einem Klick auf OK erscheint ein weißes Analysefenster. Nichts passiert. Im Menü AC starten Sie nun Run oder drücken F2. Danach sollte es etwa so aussehen wie in Bild 7. Variieren Sie nun statt des Kondensators den Widerstand zwischen 1k und 20k in 1k-Schritten und betrachten das Ergebnis, wiederum eine Kurvenschar. Falls Sie keine Kurvenschar sehen, prüfen Sie, ob Sie bei Step It ein Häkchen gesetzt haben. Fahren Sie mit der Maus über die Kurven, um den zu einer Kurve gehörenden Widerstandswert zu erfahren.

Bild 8: Variiert man die Werte von R und C in einer Analyse, erzeugt MicroCAP auf Wunsch einen dreidimensionalen Plot.
Das Stepping – also die vom Benutzer gezielte Variation der Werte einer oder mehrerer Bauelemente – steht in allen Analysen zur Verfügung. Bei einer Transientenanalyse könnten Sie zum Spaß die Frequenz der Sinusquelle V1 variieren und so eine interessante Sinuskurvenschar erzeugen und prüfen, an welchen Frequenzen sich Kurven schneiden.
Monte-Carlo
Bei der Monte-Carlo-Analyse werden mehrere Durchläufe durchgeführt. Für jeden Durchlauf wird eine neue Schaltung (circuit) erzeugt, deren numerische Parameterwerte zufällig ausgewählt werden. Den Bauteilen zugeordnete Toleranzen werden dabei auf die Bauteilewerte angewandt. Modellparameter können relative DEV- und absolute LOT-Toleranzen besitzen. Symbolische Parameter wie Batterien, Spannungs- und Stromquellen können nur LOT-Toleranzen aufweisen. Toleranzen werden als Istwert oder als Prozentsatz des nominalen Parameterwertes angegeben. Eine LOT-Toleranz wird absolut auf jedes Gerät angewendet. Die Monte Carlo-Analyse ist in den Analysen Transient, AC, und DC verfügbar.

Bild 9: Der Monte-Carlo-Optionern-Dialog. Für unser Beispiel übernehmen Sie bitte die Einstellunge.
Führen Sie zunächst eine AC-Analyse ohne Stepping aus. Sollte Stepping aktiviert sein, ist im Limits-Fenster (Bild 4) der Button Stepping fettgedruckt zu sehen. Ist das der Fall, öffnen Sie den Stepping-Dialog und klicken dort auf All Off. Nach der AC-Analyse sehen Sie – wie oben beschrieben - die Graphen des Tiefpassfilters (Bild 5). Zur Monte-Carlo-Analyse müssen den Bauelementen eine Toleranz zugewiesen werden. Gehen Sie wie folgt vor: Im Menü Monte Carlo wählen Sie Options. Im aufpoppenden Dialog stellen Sie die Werte bitte so ein, wie in Bild 9 zu sehen ist. Die Verteilung (Distribution) ist auf Worst Case eingestellt, um maximale Toleranzen zu verwenden. Mit Seed = 2 wird ein Zufallszahlengenerator gesetzt.

Bild 10: In diesem Dialog weisen wir dem Kondensator eine großzügige Toleranz zu …
Rufen Sie über den Button Tolerance den Dialog zur Einstellung der Bauteiltoleranzen auf (Bild 10). In dieser Abbildung wurde die Toleranz des Kondensators bereits auf 20% gesetzt. Wählen Sie im Kasten Types CAPACITOR, unter Models (C1) und bei Parameters C=1. Falls Sie in einem Dialog nach einer Bezeichnung für das Model zu C1 gefragt werden, vergeben Sie eine Bezeichnung wie z. B. CAP1. Nach der Auswahl in den drei Kästen wie in der Abbildung wird im Dialog der Bereich LOT veränderbar. Tragen Sie unter Tolerance 20% ein und betätigen den Apply-Button. Es sollte nun exakt so aussehen wie in Bild 10, das bedeutet, dass unter Parameters die blau markierte Zeile C=1 LOT=20% lautet.
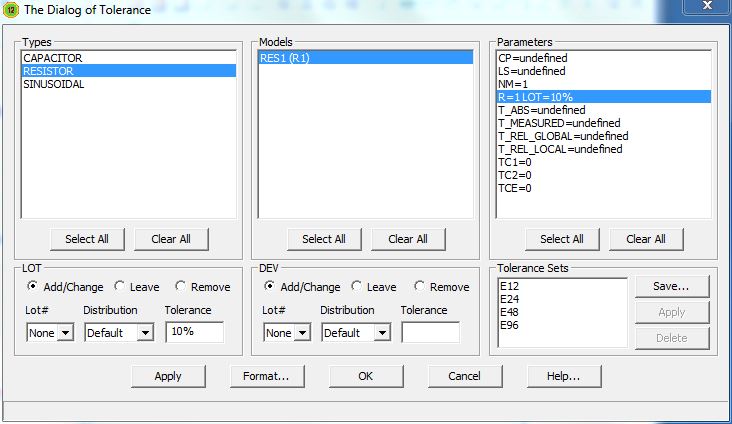
Bild 11: … und die Toleranz für den Widerstand. So muss es unter Parameters aussehen.
Dasselbe führen Sie nun für den Widerstand R1 aus, siehe Bild 11. Anschließend sind die Toleranzen festgelegt und wir verlassen den Dialog mit OK. Stören Sie sich nicht daran, dass eine Toleranz von 20% für einen Widerstand unrealistisch ist, wir wollen doch eine hübsche Grafik erzeugen, deren Kurven man unterscheiden kann. Den noch offenen Dialog Monte Carlo Options können wir nun ebenfalls mit OK verlassen.

Bild 12: Das Resultat der Mühen: die Monte-Carlo-Analyse mit Extremwerten für den Worst-Case-Fall.
Starten Sie die Analyse erneut mit F2. Es sollten nun einige Kurven erscheinen, wie Bild 12 illustriert. Als Monte-Carlo-Verteilung haben wir Worst Case gewählt. Es stehen andere Verteilungen wie Uniform und Gauss zur Verfügung.
- Uniform: Es besteht eine gleiche Verteilung bei gleicher Wahrscheinlichkeit innerhalb der Toleranzgrenzen. Jeder Wert vom Minimum bis zum Maximum ist gleich wahrscheinlich.
- Gauss: Wie der Name bereits ausdrückt, folgt die Wahrscheinlichkeit der Gaussschen Normalverteilung.
- Die Worst-Case-Verteilungen weisen eine 50%ige Wahrscheinlichkeit, das Minimum und eine 50%ige Wahrscheinlichkeit, das Maximum zu produzieren. Sie orientiert sich also an den Toleranzgrenzen.
- Variieren Sie nun die Toleranzen der Monte-Carlo-Analyse und schauen, wie sie sich auf die Kurvenschar auswirken.
Zahlreiche Beispielschaltungen (im Unterverzeichnis DATA) laden zum Lernen und Ausprobieren ein. Auf diese Beispiele beziehen sich die Erklärungen in den PDF-Dateien zum User Guide und der Referenz. Bild 13 zeigt beispielhaft eine PLL und deren Transienten-Analyse.
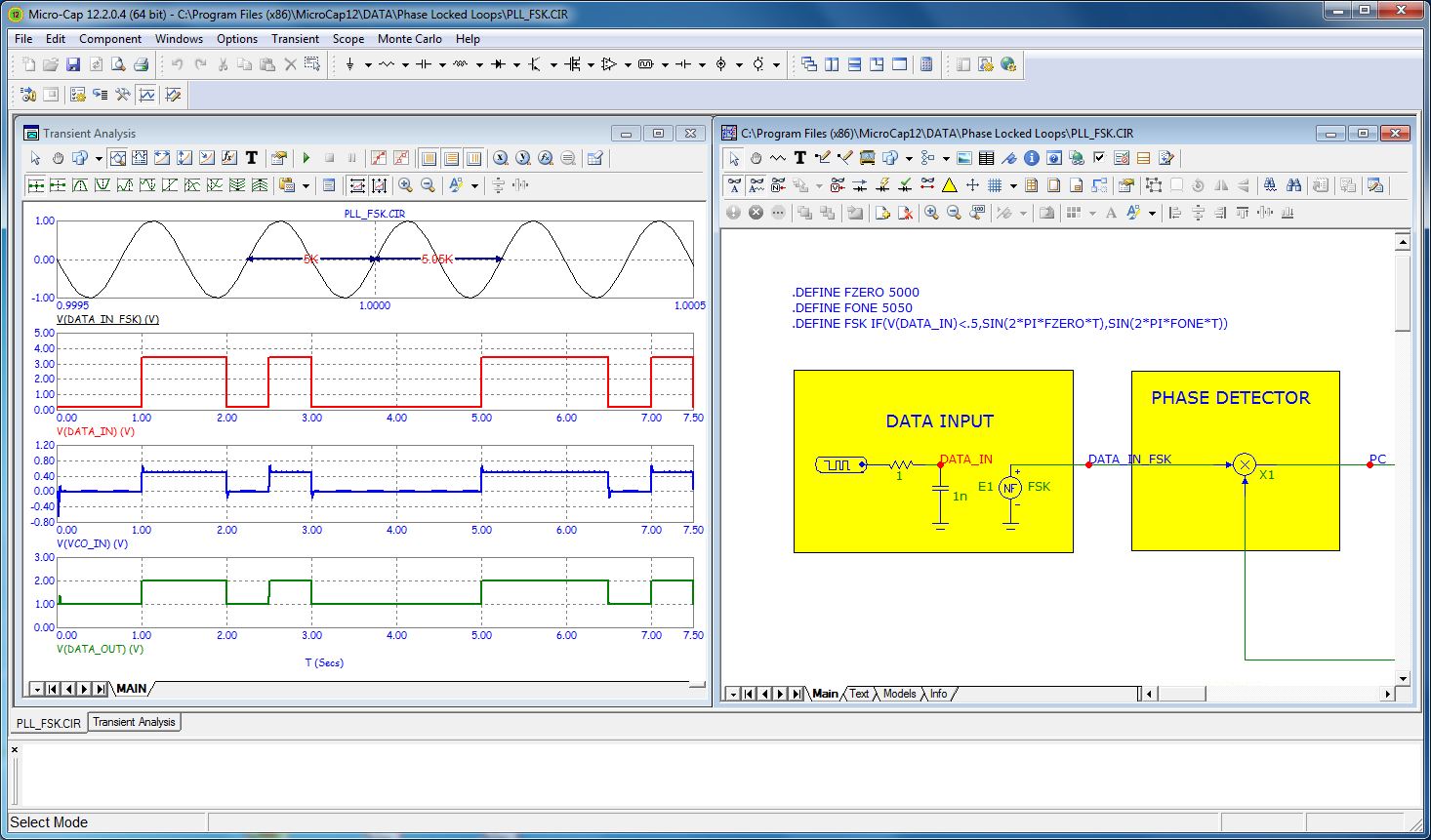
Bild 13: Viele Beispielanwendungen laden zum Lernen ein wie hier ein Beispiel zur PLL.
Abgesang
Hier steht kein Fazit, denn das wäre unangebracht, schließlich haben wir nur ein wenig an der Benutzeroberfläche gekratzt. Die Arbeit und das Lernen mit MicroCAP 12 hat dem Schreiber dieser Zeilen aber Spaß gemacht. Erstaunlich, dass man sich mehrere Tage jeweils mehrere Stunden mit der Analyse von nur drei Bauelementen beschäftigen kann! Die Leistungsvielfalt des Programms ist anfangs unüberschaubar. Je mehr man in die Tiefe vordringt, desto mehr Freude hat man mit dieser Software – und ein wenig mehr Durchblick.
Literatur/Verweise:
[1] MicroCAP 12, Homepage: http://www.spectrum-soft.com/index.shtm
[2] MicroCAP 12, Download: http://www.spectrum-soft.com/download/download.shtm
[3] MicroCAP 12, Neues: http://www.spectrum-soft.com/features.shtm
(( Bild 13 PLL))
lkökök
Mehr Zeugs
- Schaun mer mal
- Moin
- Bast scho
Hier gibt es was zu lesen
- dl1dmw.darc.de
- dl1dmw.wordpress.com
- qsl.net/dg5dbz
Adresse etc.
- Op: Michael, DL1DMW
- ITU Region 1, Zone 14, DL, JO41CO
- Bad Sassendorf
- NRW / Germany